This is the Medium-Hard side, the creator of BDHIJL.

Part of my fault for the wrong schedule for question C. Originally, this was a simpler geometry problem, but in order to balance the difficulty, the meaning of the problem was slightly modified. It is not correct to apply the correct method of the original question to this question (if it is greater than$180^\circ$180^\circwhen). It is true that the questioning process is not standardized, and there is no good verification method. On the other hand, shortage of manpower (almost only two available labor qwq) is also one of the objective reasons.

My apologies to all contestants affected by Question C.

These questions are some interesting ideas I have accumulated over the past few months. In addition to the two temporarily added code questions, the remaining few questions are still very interesting qwq, but it is really difficult to put them in the CCPC sub-station, and the discrimination is not as good as expected.

Now this set of questions (except C) has been uploaded to Gym, and you can VP or submit questions on it. Hope to continue to play the value of these topics.

Below I will add more detailed solutions to these questions, as well as some of my views. Teams with training needs please do not check the solutions below.

B. Bounding Wall

A well-regulated data structure question.

First find that we can$\mathcal{O}(n+m)$\mathcal{O}(n+m)Quickly maintains the length of white space that each square extends up/down/left/right. Suppose the currently queried block$(i,j)$(i,j)On the lower boundary, we enumerate the points corresponding to the upper boundary$(k,j)\ (k \le i)$(k,j)\ (k \le i). We also need a vertical border. We can find that the left and right sides are independent, and we can handle them separately. according to$k$kenumeration in descending order, starting with$(i,p)$(i,p)The vertical border extending upward will disappear at some point. At the same time the first$i$iline and number$k$kThe line also has the most extended length, so it becomes a vertical border asking if the prefix/suffix still exists. Binary using tree arrays$\mathcal{O}((n+m)q\log(n+m))$\mathcal{O}((n+m)q\log(n+m))You can pass this question. The standard calculation uses the union search to point to the nearest survival point, and the time complexity is$\mathcal{O}((n+m)q\alpha(n+m))$\mathcal{O}((n+m)q\alpha(n+m)).

D. Defend City

My favorite question, maybe I will never be able to come up with such a good question in my lifetime. The meaning of the question itself is very simple: there are four kinds of points in the plane covering a certain direction$1/4$1/4Plane, ask how many points can cover the entire plane at least.

All four directions require at least one point, and we record the point sets in the four directions as$P_1,P_2,P_3,P_4$P_1,P_2,P_3,P_4. For each point set, obviously only the points that are not covered by other points in the point set need to be left, and the remaining points$y$ywith$x$xincreases and changes monotonically. Let each direction choose a subset $Q_i\subseteq P_i$Q_i\subseteq P_i. Assume$Q_i$Q_iThe combined coverage area is$S_i$S_i,Assume$P_i$P_iThe combined coverage area is$T_i$T_i.

Conclusion: There exists an optimal solution such that$|Q_1|=|Q_3|=1$|Q_1|=|Q_3|=1or$|Q_2|=|Q_4|=1$|Q_2|=|Q_4|=1.

Consider an optimal solution, assuming$Q_1\ge 2$Q_1\ge 2, any pair of adjacent points$p,q$p,q, observe the intersection of their covered areas$r$r. if$r$rquilt$Q_2$Q_2or$Q_4$Q_4Points in the coverage, obviously$Q_1$Q_1Deleting a point in can still cover the entire plane, contradicting the premise. So$Q_1$Q_1The intersection of all coverage areas in$r_i$r_ican only be$Q_3$Q_3point coverage in . in turn,$Q_3$Q_3with$Q_1$Q_1the same way. consider later$Q_1,Q_3$Q_1,Q_3The intersection point of the leftmost coverage area can cover all$Q_2$Q_2The area that needs to be covered, that is,$Q_2,Q_4$Q_2,Q_4There is only one point.

Next may wish to make$|Q_2|=|Q_4| = 1$|Q_2|=|Q_4| = 1,at this time$S_1$S_1and$S_3$S_3The intersection point of the contour lines to fall into$T_2$T_2and$T_4$T_4among, and$S_3$S_3Contours are always on$S_1$S_1Right and above the outline.

May wish to enumerate$Q_1$Q_1The top point, we can greedily take the best$Q_3$Q_3The topmost point, the successor, is unique. same$Q_3$Q_3A point in also has a unique successor. Keep choosing the only successor until the$T_4$T_4There is an intersection in .

Using doubling , one can do$\mathcal{O}(n \log n)$\mathcal{O}(n \log n)time complexity.

We can prove that when the answer$\ge 5$\ge 5, the optimal solution$Q_1$Q_1top point$p_k$p_konly one. which is$T_1$T_1and$T_2$T_2Contour intersection point, the point on the left or below (according to the direction of intersection).

for$P_1$P_1middle$y$ybigger point$p_t$p_t, obviously the newly added coverage area is$p_k$p_kSubsets of new coverage areas are added. for$y$ysmaller point$p_t$p_t, will make the corresponding in$P_3$P_3successor in$p_s$p_sworse. after$p_s$p_sexist$P_1$P_1The successor in$p_k$p_kNothing to do.

find this point$p_k$p_kcan directly$\mathcal{O}(n)$\mathcal{O}(n)simulated.

H. Holy Sequence

Examines familiarity with counting DPs and use of combined meaning.

Consider the DP equation for Stirling numbers of the second kind:$s[i][j]=s[i-1][j-1]+s[i-1][j]*j$s[i][j]=s[i-1][j-1]+s[i-1][j]*j, to find a combination meaning for it. if transferred as$s[i-1][j-1]$s[i-1][j-1], indicating that a new number$j+1$j+1. if transferred as$s[i-1][j]*j$s[i-1][j]*jIndicates adding a$[1,j]$[1,j]number in$x$x. It can be found that any legal sequence is counted exactly once.

The transfer of DP is a DAG, then DP can be regarded as the path count of DAG, and the legal sequence and slave$(0,0)$(0,0)arrive$(n,j)$(n,j)The paths correspond one-to-one. Transfer edges are divided into two categories, which are marked here with different colors.

hypothetical figures$k$k appears in the legal sequence$x$xtimes, contributed to$x^2$x^2. Combination meanings can be considered, expressed in$x$xindivual$k$kThe number of options selected twice in . There are two types of situations: the same position is selected twice, or different positions are selected. Here we only consider how to deal with choosing two different locations.

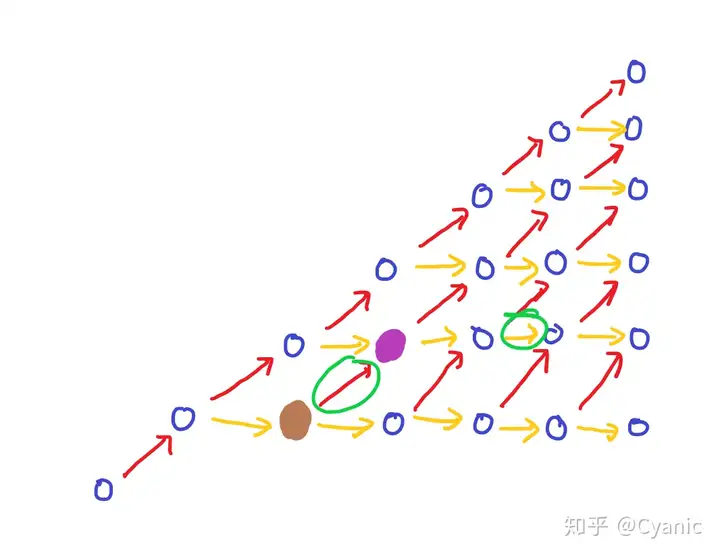
Different transfer edges correspond to different decisions (what number to put in which position). Since a certain number must not be the maximum value of the prefix after it appears for the second time , it can only be a yellow transfer edge.

In one case, as shown in the figure above, it is necessary to find the number of paths passing through these two transfer edges. Can go from left to right D$(0,0)$(0,0)Number of paths to the brown point, right to left DP$(n,j)$(n,j)to the number of purple points (additional state: whether a transfer edge is selected).

Another case is that the transfer edge on the left is a yellow transfer edge. This would make a prefixed$k$kTo make a contribution, just make a difference. The time complexity is$\mathcal{O}(n^2)$\mathcal{O}(n^2).

I. Interstellar Hunter

Comprehensive examination of basic linear algebra and number theory knowledge.

It can be proved that at any time, the reachable point set can be represented by two basis vectors . Represent the basis vectors in canonical form: one of the vectors$(d,0)\ (d \ge 0)$(d,0)\ (d \ge 0), another vector$(x,y) \ (x < d, y \ge 0)$(x,y) \ (x < d, y \ge 0). This can quickly merge after adding vectors.

Let the added vector be$(a,b)$(a,b), we can use$(a,b)$(a,b)with$(x,y)$(x,y) Linear combination out$(d',0)$(d',0), then the new$d$dthat is$\gcd(d,d')$\gcd(d,d') up. empathy new$y$yfor$\gcd(b,y)$\gcd(b,y)(vector$(d,0)$(d,0)will not contribute in this direction), use extended Euclidean to find the coefficients, and calculate the new$x$x.

special attention$d,x,y$d,x,yfor$0$0Case. The time complexity is$\mathcal{O}(n \log(x+y))$\mathcal{O}(n \log(x+y)).

J. Jewel Splitting

Various tricks for hashing…

for each$d$d, happens to have$n/d$ n/dsubsections: prefix + suffix. Calculate the hash values ​​of all prefix subsections and suffix subsections, and discretize them (in order to maintain the hash values ​​of the collection, convert them into sequence hashes). The enumeration prefix can dynamically maintain the number of occurrences of each sub-segment. In order to deduplicate, it is also necessary to maintain the hash value of the collection. Using a hash table to maintain a better time complexity requires writing a total of four different hashes. The time complexity is$O(n \log n)$O(n \log n).

L. Lost Temple

Unexpectedly, no team passed this question qwq This is a question that requires imagination owo

The key property of this question is: the difference between the answers of two adjacent columns is at most$1$1. Determine whether a column can be in$x$xDisappear after a year? Findings can be translated into whether the$i$iThe scale under the column is$x$xrhombus. It will be constrained by four directions and can be transformed into a four-time RMQ problem.

Since the answers in two adjacent columns differ by at most$1$1, we can brute force enumerate the answers based on the previous column. At the same time, it is found that the interval of RMQ query is roughly monotonous, and monotonic queue maintenance can be used, and scattered segment violence (length at most$2$2). Implementation still requires some superb skills, and at the same time maintain$4$4monotonic queue and$8$8pointer.

I'm about to retire, and I always wanted to make some small contributions to the algorithm competition circle...

Participating in the proposition of CCPC this time, even though I have some regrets, it can be regarded as a fulfillment of a small wish.

Hope you all enjoy these topics w